Topology

Introduction

Topologyisastructureonacollection.LetTbethesubsetfamilyofnon-emptysetX.IfTmeetsthefollowingconditions:

1.XandtheemptysetbelongtoT;

2.TheintersectionofanyfinitenumberofmembersinTbelongstoT;

3.TheunionofanymemberofTbelongstoT;

ThenTiscalledatopologyonX.AsetXwithatopologyTiscalledatopologicalspace,denotedas(X,T).

LetT₁andT₂bethetwotopologiesonthesetX.IfitisrelatedtoT₁T₂,thenT₁issaidtobethickerthanT₂,orT₂isthinnerthanT₁.WhentwotopologiesonXhavenocontainmentrelationshipwitheachother,theyaresaidtobeincomparable.OnsetX,discretetopologyisthefinesttopology,andtrivialtopologyisthethickesttopology.

Mathematicalterms

Axioms

LetXbeanon-emptyset,asubsetofthepowersetofX(thatis,somesubsetofXSetfamily)TiscalledatopologyofX.Ifandonlyif:

1.BothXandtheemptyset{}belongtoT;

2.TheunionofanynumberofmembersinTisstillinT;

3.TheintersectionofalimitednumberofmembersinTisstillinT.

CallthesetXanditstopologyτatopologicalspace,denotedas(X,T).

CallthemembersofTastheopensetofthistopologicalspace.

Thethreeconditionsinthedefinitionarecalledtopologicalaxioms.(Condition(3)canbeequivalentlyreplacedbytheintersectionoftwomembersinτ,whichisstillinτ.)

Fromthepointofviewofdefinition,atopologyofasetistospecifywhichsubsetsofit.Itisopenset.Theseregulationsarenotarbitrary,andmustsatisfythreetopologicalaxioms.

Generallyspeaking,manydifferenttopologiescanbespecifiedonaset,sowhentalkingaboutatopologicalspace,itisnecessarytospecifythesetandthespecifiedtopologyatthesametime.Withoutcausingmisunderstanding,asetisoftenusedtorefertoatopologicalspace,suchastopologicalspaceX,topologicalspaceY,andsoon.

Atthesametime,inthetopologicalcategory,wediscusscontinuousmapping.Itisdefinedas:f:(X,T1)------>(Y,T2)(T1,T2isthetopologydefinedabove)iscontinuousifandonlyifthepre-imageoftheopensetisopenset.Twotopologicalspacesarehomeomorphicifandonlyifthereisaone-to-onecorrespondingreciprocalcontinuousmapping.Atthesametime,mappinghomotopyandspatialhomotopyequivalencearealsousefuldefinitions.

Example

1.TheEuclideanspaceisatopologicalspaceinthesenseoftheusualopenset,anditstopologyisthesetofallopensets.

2.LetXbeanon-emptyset.Thenthesett:{X,{}}isatopologyofX.CalltthetrivialtopologyofX.Obviously(X,t)hasonlytwoopensets,Xand{}.

3.LetXbeanon-emptyset.ThenthepowersetofXT=2^XisalsoatopologyofX.CallTthediscretetopologyofX.ObviouslyanysubsetofXisanopensetof(X,T).

4.Aconcreteexample.LetX={1,2}.Then{X,{},{1}}isatopologyofX,{X,{},{2}}isalsoatopology,{X,{},{1},{2}}isatopology(asknownbythedefinition).

Origin

1.KönigsbergTheSevenBridgesProblem

Inmathematics,thesevenbridgesofKönigsberg,Euler'stheoremofpolyhedrons,andfour-colorproblemsareallimportantissuesinthehistoryoftopology.Königsberg(present-dayKaliningrad,Russia)isthecapitalofEastPrussia,andthePlegelRivertraversesit.Sevenbridgeswerebuiltonthisriverintheeighteenthcentury,connectingthetwoislandsinthemiddleoftheriverwiththebank.Peopleoftentakeawalkhereintheirleisuretime.Onedaysomeoneasked:Canyouwalkeachbridgeonlyonce,andfinallyreturntoitsoriginalposition.Thisseeminglysimpleandinterestingquestionattractedeveryone.Manypeoplearetryingvariousways,butnoonehasdoneit.Itseemsthatitisnotsoeasytogetaclearandidealanswer.

In1736,someonetookthisquestiontoEuler,agreatmathematicianatthetime.Aftersomethinking,Eulerquicklygavetheanswerinauniqueway.Eulerfirstsimplifiedthisproblem.Heregardedthetwosmallislandsandthebanksoftheriverasfourpoints,andthesevenbridgesastheconnectionbetweenthesefourpoints.Thenthequestionissimplifiedto,canthefigurebedrawninonestroke?Afterfurtheranalysis,Eulerconcludedthatitisimpossibletowalkthrougheverybridgeandfinallyreturntotheoriginalposition.Andgiventheconditionsthatallgraphicsthatcanbedrawninonestrokeshouldhave.Thisisthe"firstsign"oftopology.

2.PolyhedronEuler'sTheorem

Inthehistoryoftopology,thereisanotherfamousandimportantThetheoremaboutpolyhedronsisalsorelatedtoEuler.Thecontentofthistheoremis:Ifthenumberofverticesofaconvexpolyhedronisv,thenumberofedgesise,andthenumberoffacesisf,thentheyalwayshavethisrelationship:f+v-e=2.

AccordingtoEuler'stheoremofpolyhedrons,aninterestingfactcanbedrawn:thereareonlyfivekindsofregularpolyhedrons.

Theyareregulartetrahedron,regularhexahedron,regularoctahedron,regulardodecahedron,regularicosahedron.

3.Four-colorconjecture

Thefamous"four-colorproblem"isalsoaproblemrelatedtothedevelopmentoftopology.Thefour-colorproblem,alsoknownasthefour-colorconjecture,isoneofthethreemajormathematicalproblemsinmoderntimesintheworld.Thefour-colorconjecturecamefromtheUnitedKingdom.In1852,whenFernancisGuthrie,whograduatedfromtheUniversityofLondon,cametoascientificresearchunittodomapcoloringwork,hediscoveredaninterestingphenomenon:"Itseemsthateverymapcanbecoloredwithfourcolors,sothatCountrieswithcommonbordersareallgivendifferentcolors."

In1872,Kelly,themostfamousBritishmathematicianatthetime,formallyaskedthisquestiontotheLondonMathematicalSociety,andthefour-colorconjecturebecameworldmathematics.Issuesofconcerntotheworld.Manyfirst-classmathematiciansintheworldhaveparticipatedinthebattleofthefour-colorconjecture.Between1878and1880,famouslawyersandmathematiciansKempandTaylorrespectivelysubmittedpapersprovingthefour-colorconjectureandannouncedthattheyhadprovedthefour-colortheorem.ButlaterthemathematicianHerwoodpointedoutthatKemp'sproofwaswrongwithhisprecisecalculations.Soon,Taylor'sproofwasalsodenied.Asaresult,peoplebegantorealizethatthisseeminglyeasyproblemisactuallyadifficultproblemcomparabletoFermat'sconjecture.

Sincethebeginningofthe20thcentury,scientistshavebasicallyproceededtoprovethefour-colorconjectureinaccordancewithKemp'sideas.Aftertheadventofelectroniccomputers,duetotherapidincreaseincalculationspeedandtheemergenceofhuman-computerdialogue,theprocessofprovingthefour-colorconjecturehasbeengreatlyaccelerated.In1976,AmericanmathematiciansAppelandHarkenspent1,200hoursontwodifferentelectroniccomputersattheUniversityofIllinois,made10billionjudgments,andfinallycompletedtheproofofthefour-colortheorem.However,manyscientistsarenotsatisfiedwiththeachievementsofcomputers.Theybelievethatthereshouldbeasimpleandclearmethodofwrittenproof.

Theaboveseveralexamplestalkedaboutsomeproblemsrelatedtogeometricfigures,buttheseproblemsaredifferentfromtraditionalgeometry,butsomenewgeometricconcepts.Thesearetheprecursorsof"topology".

Definition

TheEnglishnameoftopologyisTopology,andtheliteraltranslationistopography,whichisarelateddisciplinesimilartothestudyoftopographyandlandforms.InearlyChina,itwastranslatedinto"SituationalGeometry","ContinuousGeometry",and"GeometryunderOne-to-OneContinuousTransformationGroup".However,thesetranslationnamesarenotveryeasytounderstand.Theunified"MathematicsNouns"wasunifiedin1956.Determineitastopology,whichisbasedontransliteration.

Topologyisabranchofgeometry,butthiskindofgeometryisdifferentfromtheusualplanegeometryandsolidgeometry.Theusualresearchobjectsofplanegeometryorsolidgeometryarethepositionalrelationshipbetweenpoints,linesandsurfacesandtheirmeasurementproperties.Topologyhasnothingtodowiththelength,size,area,volumeandothermetricpropertiesandquantitativerelationshipsoftheresearchobjects.

Forexample,intheusualplanegeometry,onefigureontheplaneismovedtoanotherfigure.Iftheycompletelyoverlap,thetwofiguresarecalledcongruent.However,thegraphstudiedintopologychangesregardlessofitssizeorshapeinmotion.Therearenoelementsthatcannotbebentintopology,andthesizeandshapeofeachfigurecanbechanged.Forexample,whenEulersolvedtheproblemoftheSevenBridgesofKönigsberg,hedrewgraphicswithoutconsideringitssizeandshape,onlythenumberofpointsandlines.

Properties

Thecentraltaskoftopologyistostudytheinvarianceoftopologicalproperties.

Whatarethetopologicalproperties?First,weintroducetopologicalequivalence,whichisatopologicalpropertythatisrelativelyeasytounderstand.

Intopology,theconceptofcongruenceoftwographsisnotdiscussed,buttheconceptoftopologicalequivalenceisdiscussed.Forexample,eventhoughtheshapesandsizesofcircles,squares,andtrianglesaredifferent,theyareallequivalentfiguresundertopologicaltransformation.Choosesomepointsonaspheretoconnectthemwithdisjointlines,sothatthesphereisdividedintomanypiecesbytheselines.Undertopologicaltransformation,thenumberofpoints,lines,andblocksisstillthesameastheoriginalnumber,whichistopologicalequivalence.Generallyspeaking,foraclosedsurfaceofanyshape,aslongasthesurfaceisnottornorcut,itstransformationisatopologicaltransformation,andthereistopologicalequivalence.

Itshouldbepointedoutthatthetorusdoesnothavethisproperty.Imaginethatifthetorusiscut,itwillnotbedividedintomanypieces,butitwillbecomeacurvedbarrel.Inthiscase,wesaythatthespherecannotbetopologicallyturnedintoatorus.Sothesphericalsurfaceandthetorusaredifferentsurfacesintopology.

Thecombinationandsequencerelationshipofpointsandlinesonastraightlineareunchangedundertopologicaltransformation,whichisatopologicalproperty.Intopology,theclosedpropertiesofcurvesandsurfacesarealsotopologicalproperties.

Theplaneandcurvedsurfaceweusuallytalkaboutusuallyhavetwosides,justlikeapieceofpaperhastwosides.ButtheGermanmathematicianMobius(1790～1868)discoveredtheMobiussurfacein1858.Thiskindofsurfacecannotbepaintedontwosideswithdifferentcolors.

Mobiustape

In1858,Mobiusdiscoveredthatastripofpaperthatwastwistedby180°andgluedonbothendshadmagicalproperties.Becauseordinarypapertapehastwosides(thatis,double-sidedcurvedsurfaces),onefrontsideandonereverseside,andthetwosidescanbepaintedindifferentcolors;whilesuchpapertapeshaveonlyoneside(thatis,single-sidedcurvedsurfaces),onesmallThewormcancrawlacrosstheentiresurfacewithouthavingtocrossitsedges!Wecallthismagicalsingle-sidedpapertapediscoveredbyMobiusthe"Mobiustape".

Takealongwhitepaper,paintonesideblack,turnoneendover,andglueitintoaMobiustapeasshowninFigure1.CutitalongthecenterofthetapewithscissorsasshowninFigure1.Youwillbesurprisedtofindthatnotonlyisthepapertapenotdividedintotwo,butapapercirclethatistwiceaslongasshowninFigure1iscutout!

What’sinterestingisthatthenewlyobtainedlongerpapercircleitselfisadouble-sidedcurvedsurface.Althoughitstwobordersarenotknotted,theyarenestedtogether!Inordertoletthereadersintuitivelyseethisfactthatisnoteasytoimagine,wecancuttheabovepapercircleagainalongthecenterline,thistimeitcanreallybedividedintotwo!Whatyougetaretwopapercirclesthatarenestingaroundeachother,andtheoriginaltwobordersarecontainedinthetwopapercircles,buteachpapercircleitselfisnotknotted.

Forexample,athree-leafknotwillbeformedafterabeltthatisrotatedthreeandahalfturnsandcut.Aftercuttingthetape,rotateit,andthenpasteitagain,itwillbecomeseveralParadromics.

TheMobiusstripisoftenregardedasthecreativesourceoftheinfinitysymbol"∞",becauseifsomeonestandsonthesurfaceofahugeMobiusstripalongwhathecansee""Theroad"keepsgoing,andhewillneverstop.Butthisisanuntruerumor,because"∞"wasinventedearlierthantheMobiusbelt.

TheMobiusbelthasevenmoreexoticcharacteristics.SomeproblemsthatcouldnotbesolvedontheplaneweresolvedincredibleontheMobiusbelt!

Forexample,theproblemofglovetranslocationthatcannotbeachievedinordinaryspace:Althoughtheglovesoftheleftandrighthandsofapersonareverysimilar,theyarefundamentallydifferent.Itisimpossibleforustoputthegloveofthelefthandontherighthand;norcanweputthegloveoftherighthandonthelefthand.Nomatterhowyoutwistaround,theleftglovewillalwaysbetheleftglove,andtherightglovewillalwaysbetherightglove!However,ifyoubroughtittoMobius,itwillbeeasytosolve.

Therearemanyobjectsinnaturethataresimilartogloves.Theyhavecompletelysimilarsymmetricalparts,butoneisleft-handedandtheotherisright-handed.Thereisahugedifferencebetweenthem.

The"Mobiusbelt"hassomeusesinlifeandproduction.Forexample,thebeltofapowermachinethatisconveyedbyabeltcanbemadeintoa"Mobiusbelt"sothatthebeltwillnotonlywearoutononeside.Ifthetapeofthetaperecorderismadeintoa"Mobiustape",therewillbenoproblemofbothsides,andthetapewillhaveonlyoneside.

RubberGeometry

TheMobiusstripisatopologicalfigure.Whatistopology?Topologystudiessomepropertiesofgeometricfigures.Theyremainunchangedwhenthefigureisbent,enlarged,reducedorarbitrarilydeformed.Aslongastheoriginaldifferentpointsarenotoverlappedintothesamepointduringthedeformationprocess,theywillnotproduceNewpoint.Inotherwords,theconditionofthistransformationisthatthereisaone-to-onecorrespondencebetweenthepointsoftheoriginalfigureandthepointsofthetransformedfigure,andtheadjacentpointsarestilladjacentpoints.Suchtransformationiscalledtopologicaltransformation.Thereisanimageoftopology-rubbergeometry.Becauseifthegraphicsareallmadeofrubber,manygraphicscanbetopologicallytransformed.Forexample,arubberbandcanbetransformedintoacircleorasquarecircle.ButarubberbandcannotbetransformedintoanArabicnumeral8bytopologicaltransformation.Becausethetwopointsonthecirclearenotoverlapped,thecirclewillnotbecome8,andthe"Mobiusbelt"justmeetstheaboverequirements.Therearemanyinvariancesandinvariantsoftopologicaltransformation,whichwillnotbeintroducedhere.

Topology

Aftertheestablishmentoftopology,duetothedevelopmentneedsofothermathematicsdisciplines,ithasalsobeendevelopedrapidly.EspeciallyafterRiemannfoundedRiemanniangeometry,hetooktheconceptoftopologyasthebasisofanalysisfunctiontheory,whichfurtherpromotedtheprogressoftopology.

Sincethe20thcentury,settheoryhasbeenintroducedintotopology,openingupanewlookfortopology.Thestudyoftopologyhasbecomeaconceptaboutthecorrespondenceofanarbitrarysetofpoints.Someproblemsintopologythatrequireprecisedescriptioncanbediscussedusingsets.

Becauseofthecontinuityofalargenumberofnaturalphenomena,topologyhasthepossibilityofextensivelyconnectingvariouspracticalthings.Throughthestudyoftopology,thesetstructureofspacecanbeclarified,andthefunctionalrelationshipbetweenspacescanbegrasped.Sincethe1930s,mathematicianshavemademorein-depthresearchontopologyandputforwardmanynewconcepts.Forexample,theconceptofconsistentstructure,abstractdistanceandapproximatespaceconcept,andsoon.Thereisabranchofmathematicscalleddifferentialgeometry,whichusesdifferentialtoolstostudythebendingofcurvesandsurfacesnearapoint,whiletopologystudiestheglobalconnectionofsurfaces.Therefore,thereshouldbeacertainessentialconnectionbetweenthetwodisciplines..In1945,theAmericanChinesemathematicianChenXingshenestablishedtheconnectionbetweenalgebraictopologyanddifferentialgeometry,andpromotedthedevelopmentofoverallgeometry.

Today,topologyhasdevelopedintotwobranchesintheory.Abranchisfocusedontheuseofanalyticalmethods,calledpointsettopology,orcalledanalyticaltopology.Anotherbranchisfocusedonusingalgebraicmethodstostudy,calledalgebraictopology.Now,thesetwobrancheshaveaunifiedtrend.

Topologyhasawiderangeofapplicationsinfunctionalanalysis,Liegrouptheory,differentialgeometry,differentialequationsandmanyotherbranchesofmathematics.

Artterms

Take3DSMAXsoftwareasanexample.Aftercreatingobjectsandgraphics,eachvertexand/orfacewillbeassignedanumber.Usually,thesenumbersareusedinternally,andtheycandeterminetheverticesorfacesselectedataspecifiedtime.Thisnumericalstructureiscalledtopology.

Afterselectingavertexorfaceandapplyingamodifiertotheselectedobject,themodifierstackwillrecordthefaces/verticesitaffects.Ifyoureturntothestackselectionlevellater,youcanchangethetopologytoapplythemodifier.

Thetermtopologyreferstothestructureandnumberingoffacesandvertices.

Forexample,bycarefullysettingvariousparameters,youcanmaketheboxandthecylinderhavethesamenumberofvertices.Afterthat,youmightthinkthatyoucanusetheboxasadeformationtargetforthecylinder.However,becausethesetwoobjectsarecreatedusingverydifferentmethods,theorderofthevertexnumbersoftheseobjectswillbequitedifferent.Ifthedeformationisperformed,eachnumberedvertexwillbeturnedtothecorrespondingpositiononthedeformationtarget.Inthiscase,therearetwoobjectswithverydifferenttopologicalstructures.Ifyoudeformfromoneobjecttoanother,theobjectwillbendorturninsideoutwhendeformed.

Topology-relatedmodifierscanperformselectionoperationsonexplicitsub-objectswithtopologicalstructure.Modifiersforperformingoperationsorselectionsonexplicitverticesorfacesincludethe"EditMesh"and"MeshSelection"modifiers.Whenthesemodifiersareincludedinthestack,ifyouaccessthepreviousstackoperationandchangethetopology(thenumberandorderoffacesandvertices)passedtoit,theresultsmaybenegativelyaffected.Ifyoudothis,topologyrelatedwarningswillpromptyoutopayattentiontothissituation.

Toputitsimply,theso-calledtopologyistoredrawthemodelontheoriginalbasistoproduceaveryefficientmodel.Letthemodeldetailsenoughandthenumberoffacesisverysmall.Itwillhelpustomakeadvancedanimationinthefuture.Sothehigh-precisionmodelproducedbyZBrushcannotbeused.

Note:Topologyisalsocalledtopology

networkterminology

Interpretation

computernetworktopologyItisamethodtostudytherelationshipbetweenpointsandlinesthathavenothingtodowithsizeandshapeintopology.Thecomputerandcommunicationequipmentinthenetworkareabstractedasapoint,andthetransmissionmediumisabstractedasaline.Thegeometricfigurecomposedofpointsandlinesisthetopologicalstructureofthecomputernetwork.Thetopologicalstructureofthenetworkreflectsthestructuralrelationshipoftheentitiesinthenetwork.Itisthefirststepinbuildingacomputernetworkandthebasisfortherealizationofvariousnetworkprotocols.Ithasasignificantimpactontheperformanceofthenetwork,thereliabilityofthesystemandthecommunicationcost.Topologyinacomputernetworkreferstotheformandmethodofconnectingnodes.

Thenetworkunitssuchasworkstationsandserversinthenetworkareabstractedas"dots".Thecablesandthelikeinthenetworkareabstractedas"lines".Affectnetworkperformance,systemreliability,andcommunicationcosts.

Classification

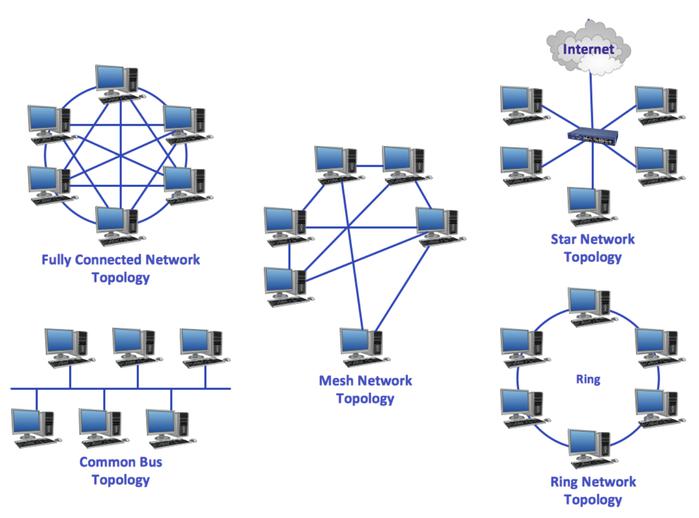
1.Bustopology

ThebustopologyistocombinealldevicesinthenetworkItisdirectlyconnectedtothepublicbusthroughthecorrespondinghardwareinterface,andthenodescommunicateinabroadcastmode.Theinformationsentbyonenodecanbe"listened"toothernodesonthebus.Advantages:simplestructure,easywiring,highreliability,andeasytoexpand.Itisatopologicalstructureoftenusedinlocalareanetworks.Disadvantages:Alldataneedstobetransmittedthroughthebus,andthebusbecomesthebottleneckoftheentirenetwork;itismoredifficulttodiagnosefaults.ThemostfamousbustopologyisEthernet.

2.Startopology

Eachnodeisconnectedtothecentralnodebyaseparatecommunicationline.Advantages:simplestructure,easytoimplement,easytomanage,andeasytomonitorandeliminatethefailureoftheconnectionpoint.Disadvantages:Thecentralnodeisthereliablebottleneckoftheentirenetwork,andthefailureofthecentralnodewillcausethenetworktobeparalyzed.

3.Ringtopology

Eachnodeformsaclosedloopthroughcommunicationlines,anddataintheringcanonlybetransmittedinonedirection.Advantages:simplestructure,easytoimplement,suitablefortheuseofopticalfiber,longtransmissiondistance,anddefinitetransmissiondelay.Disadvantages:Eachnodeintheringnetworkbecomesthebottleneckofnetworkreliability,anynodefailurewillcausethenetworktobeparalyzed,andfaultdiagnosisisalsodifficult.ThemostfamousringtopologynetworkisTokenRing.

4.Treetopology

YesAhierarchicalstructureinwhichnodesareconnectedbylayers.Informationexchangeismainlycarriedoutbetweenupperandlowernodes,anddataexchangeisgenerallynotcarriedoutbetweenadjacentnodesornodesatthesamelevel.Advantages:simpleconnection,convenientmaintenance,suitableforapplicationrequirementsforgatheringinformation.Disadvantages:Theresourcesharingabilityislow,andthereliabilityisnothigh.Thefailureofanyworkstationorlinkwillaffecttheoperationoftheentirenetwork.

5.Meshtopology

Alsocalledirregularstructure,theconnectionbetweennodesisarbitrary,irregular.Advantages:Thesystemhashighreliabilityandisrelativelyeasytoexpand,butthestructureiscomplex,andeachnodeisconnectedtomultiplepoints,soroutingalgorithmsandflowcontrolmethodsmustbeused.Thecurrentwideareanetworkbasicallyusesameshtopology.

Topologyinphysics

Inphysics,topologyisusedinseveralfields,suchascondensedmatterphysics,quantumfieldtheory,andphysicalcosmology.

Thetopologicaldependenceofmechanicalpropertiesinsolidsisofinterestinthedisciplinesofmechanicalengineeringandmaterialsscience.Electricalandmechanicalpropertiesdependonthearrangementandnetworkstructureofmoleculesandbasicunitsinthematerial.Thecompressivestrengthofthefoldtopologywasstudied,tryingtounderstandthehigh-strengthweightofthisstructure,whichismainlyemptyspace.Topologyisofgreatsignificanceincontactmechanics,wherethedependenceofstiffnessandfrictiononthedimensionalityofthesurfacestructureisthefocusofapplicationinmultibodyphysics.

Topologicalquantumfieldtheory(ortopologicalfieldtheoryorTQFT)isaquantumfieldtheoryforcalculatingtopologicalinvariants.

AlthoughTQFTwasinventedbyphysicists,theyalsohavemathematicalinterests,includingknottheoryandfour-divisionmanagementtheoryinalgebraictopology,andmodularspacetheoryinalgebraicgeometry.Donaldson,Jones,Witten,andKontevichhaveallreceivedfieldmedalsrelatedtotopologicalfieldtheory.

ThetopologicalclassificationoftheCalabi-Yaumanifoldisofgreatsignificanceinstringtheory,becausedifferentmanifoldscanwithstanddifferentkindsofstrings.

Incosmology,topologycanbeusedtodescribetheoverallshapeoftheuniverse.Thisareaiscalledspatio-temporaltopology.

Topologyintherobot

Thevariouspossiblepositionsoftherobotcanbedescribedbyamanifoldcalledtheconfigurationspace.Inthefieldofmotionplanning,thepathbetweentwopointscanbefoundintheconfigurationspace.Thesepathsrepresentthemovementoftherobot'sjointsandotherpartsintothedesiredpositionandposture.