Introduction
RSApublickeycryptosystemisamethodthatusesdifferentencryptionkeysanddecryptionkeys."Decryptionisderivedfromknownencryptionkeys.Thekeyiscomputationallyinfeasible"cryptographicsystem."
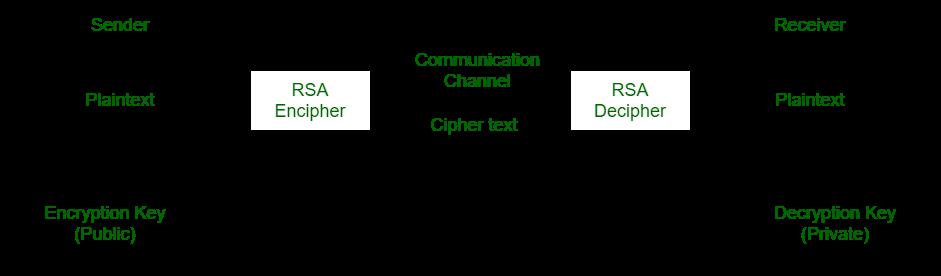
Inthepublickeycryptosystem,theencryptionkey(thatis,thepublickey)PKispublicinformation,andthedecryptionkey(thatis,thesecretkey)SKneedstobekeptsecret.EncryptionalgorithmEanddecryptionalgorithmDarealsopublic.AlthoughthedecryptionkeySKisdeterminedbythepublickeyPK,SKcannotbecalculatedbasedonPK.
Basedonthistheory,thefamousRSAalgorithmappearedin1978.ItusuallygeneratesapairofRSAkeysfirst,oneofwhichisasecretkey,whichiskeptbytheuser;theotherisapublicsecret.Thekeycanbedisclosedtotheoutsideworldandcanevenberegisteredinawebserver.Inordertoimprovethesecuritystrength,theRSAkeyisatleast500bitslong,and1024bitsaregenerallyrecommended.Thismakesencryptioncomputationallyexpensive.Inordertoreducetheamountofcalculation,whentransmittinginformation,acombinationoftraditionalencryptionmethodsandpublickeyencryptionmethodsisoftenused,thatis,theinformationisencryptedwithanimprovedDESorIDEAconversationkey,andthentheRSAkeyisusedtoencrypttheconversationkeyandinformationSummary.Aftertheotherpartyreceivestheinformation,itcandecryptitwithadifferentkeyandcanchecktheinformationdigest.
RSAisthemostwidelystudiedpublickeyalgorithm.Ithasbeennearly30yearssinceitwasproposed.Ithasundergonevariousattacksandhasgraduallybeenacceptedbypeople.Itisgenerallyregardedasthebestpublickeyalgorithmcurrently.Oneofthekeyschemes.In1983,theMassachusettsInstituteofTechnologyappliedforapatentfortheRSAalgorithmintheUnitedStates.
RSAallowsyoutochoosethesizeofthepublickey.A512-bitkeyisconsideredinsecure;a768-bitkeydoesnothavetoworryaboutbeingcompromisedbyanythingotherthantheNationalSecurityAdministration(NSA);a1024-bitkeyisalmostsafe.RSAisembeddedinsomemajorproducts,suchasWindows,NetscapeNavigator,QuickenandLotusNotes.
PrincipleofAlgorithm
TheprincipleofRSApublickeycryptosystemis:Accordingtonumbertheory,itisrelativelysimpletofindtwolargeprimenumbers,butitisextremelydifficulttofactorizetheirproduct.Therefore,theproductcanbedisclosedasanencryptionkey.
Algorithmdescription
ThespecificdescriptionoftheRSAalgorithmisasfollows:
(1)Calculatetheproductoftwodifferentlargeprimenumberspandqarbitrarily;
(2)Choosealargeintegerearbitrarily,satisfying,andtheintegereisusedastheencryptionkey(note:theselectionofeiseasy,forexample,Allprimenumbersgreaterthanpandqareavailable);
(3)Thedetermineddecryptionkeydsatisfies,thatis,isanarbitraryinteger;Therefore,ifyouknoweand,itiseasytocalculated;
(4)Opentheintegersnande,andkeepdsecretly;
(5)Decrypttheplaintextm(m
(6)Decrypttheciphertextcintoplaintextm,thedecryptionalgorithmis
However,itisimpossibletocalculatedbasedononlynande(note:notpandq).Therefore,anyonecanencrypttheplaintext,butonlyOnlyauthorizedusers(knowingd)candecrypttheciphertext.
Security
ThesecurityofRSAdependsonthedecompositionoflargenumbers,butwhetheritisequivalenttothedecompositionoflargenumbershasnotbeenobtained.Thetheoreticalproofdoesnotprovetodeciphertheoretically.ThedifficultyofRSAisequivalenttothedifficultyofdecompositionoflargenumbers.BecausethereisnoproofthatcrackingRSArequiresdecompositionoflargenumbers.Assumingthereisanalgorithmthatdoesnotrequiredecompositionoflargenumbers,thenItcandefinitelybemodifiedintoalargenumberdecompositionalgorithm,thatis,themajorflawofRSAisthatitisimpossibletograspitsconfidentialityperformancetheoretically,andmostpeopleincryptographytendtofactorizationisnotaNPCproblem.
Currently,RSASomevariantsofthealgorithmhavebeenprovedtobeequivalenttothedecompositionoflargenumbers.Inanycase,decompositionofnisthemostobviousattackmethod.Now,peoplehavebeenabletodecomposelargeprimenumberswithmorethan140decimalplaces.Therefore,themodulusnmustbeselectedlarger,Dependingonthespecificapplication.
ThesecuritystrengthoftheRSAalgorithmincreasesasthelengthofitskeyincreases.However,thelongerthekey,thelongerittakestoencryptanddecrypt.Therefore.,Itmustbeconsideredbasedonthesensitivityoftheprotectedinformation,thecostoftheattacker’scracking,andthereactiontimerequiredbythesystem,especiallyinthefieldofbusinessinformation.
Computationspeed
Becauseallcalculationsareperformedonlargenumbers,thefastestcaseofRSAisalsoseveraltimesslowerthanDES,whetheritisimplementedinsoftwareorhardware.SpeedhasalwaysbeenadefectofRSA.Generallyspeaking,itisonlyusedforsmallamounts.Dataencryption.ThespeedofRSAissymmetricalthanthatofthecorrespondingsecuritylevelTheencryptionalgorithmisabout1000timesslower.
Algorithmicattacks
Sofar,therehavebeenmanyattacksonRSA,butnoneofthemposesarealthreattoit.Here,wediscusssometypicalattackmethods.
RSA'schoiceofpasswordattack
RSAisveryvulnerableinthefaceofchoiceofpasswordattack.Generally,anattackerdisguisesacertainpieceofinformationandallowstheentitypossessingtheprivatekeytosignit;then,aftercalculation,theinformationitwantscanbeobtained.Infact,theattacksexploitthesameweakness,thatis,thefactthatthepowerpreservesthemultiplicationstructureoftheinput.Asmentionedearlier,thisinherentproblemcomesfromthemostbasicfeatureofthepublickeycryptosystem,thatis,everyonecanusethepublickeytoencryptinformation.Thisproblemcannotbesolvedalgorithmically.Therearetwoimprovementmeasures:useagoodpublickeyprotocoltoensurethattheentitydoesnotdecrypttheinformationarbitrarilygeneratedbyotherentitiesduringtheworkprocess,anddoesnotsigninformationthatitdoesnotknow;thesecondisneverright.Arandomdocumentsentbyastrangerissigned,orthedocumentishashedfirstwhensigning,ordifferentsignaturealgorithmsareusedatthesametime.
RSA'ssmallexponentattack
Whenthepublickeyetakesasmallvalue,althoughtheencryptionbecomeseasiertoimplementandthespeedincreases,itisnotsafetodoso..Theeasiestwayistotakelargervaluesforbotheandd.
Becausethekeygenerationisrestrictedbytheprimenumbergenerationtechnology,italsohasitslimitations.
(1)Thegenerationofthekeyisrestrictedbytheprimenumbergenerationtechnology,soitisdifficulttoachieveonekeyatatime;
(2)Thepacketlengthistoolarge,inordertoensuresecurity,nAtleast600bitsormore,makingthecalculationcostveryhigh,especiallytheslowerspeed,severalordersofmagnitudeslowerthanthesymmetricencryptionalgorithm;withtheimprovementoftheprimefactorizationalgorithmoflargeintegersandtheimprovementofcomputercomputingpower,thelengthofnisconstantlychangingTheincreaseisnotconducivetothestandardizationofdataformats.
