Difference
Thedifferencebetweenclusteringandclassificationisthattherequiredclassofclusteringisunknown.
Clusteringisaprocessofclassifyingdataintodifferentclassesorclusters,soobjectsinthesameclusterhavegreatsimilarities,whileobjectsindifferentclustershavegreatdissimilarities.
Fromastatisticalpointofview,clusteranalysisisamethodofsimplifyingdatathroughdatamodeling.Traditionalstatisticalclusteranalysismethodsincludesystematicclustering,decomposition,addition,dynamicclustering,orderedsampleclustering,overlappingclusteringandfuzzyclustering.Clusteranalysistoolsusingk-means,k-centerpointsandotheralgorithmshavebeenaddedtomanywell-knownstatisticalanalysissoftwarepackages,suchasSPSS,SAS,etc.
Fromtheperspectiveofmachinelearning,clustersareequivalenttohiddenmodes.Clusteringisanunsupervisedlearningprocessofsearchingforclusters.Unlikeclassification,unsupervisedlearningdoesnotrelyonpre-definedclassesortrainingexampleswithclassmarks.Theclusteringlearningalgorithmneedstoautomaticallydeterminethelabels,whiletheexamplesordataobjectsofclassificationlearninghavecategorylabels.Clusteringisobservationallearning,notexemplarylearning.
Clusteranalysisisanexploratoryanalysis.Intheprocessofclassification,peopledonotneedtogiveaclassificationstandardinadvance.Clusteranalysiscanstartfromsampledataandautomaticallyclassify.Differentmethodsusedinclusteranalysisoftenleadtodifferentconclusions.Differentresearchersperformclusteranalysisonthesamesetofdata,andthenumberofclustersobtainedmaynotbethesame.
Fromtheperspectiveofpracticalapplications,clusteranalysisisoneofthemaintasksofdatamining.Moreover,clusteringcanbeusedasanindependenttooltoobtainthedistributionofdata,observethecharacteristicsofeachclusterofdata,andfocusonspecificclustersforfurtheranalysis.Clusteranalysiscanalsobeusedasapreprocessingstepforotheralgorithms(suchasclassificationandqualitativeinductionalgorithms).
Definition
Accordingtothecharacteristicsofresearchobjects(samplesorindicators),themethodofclassifyingthemcanreducethenumberofresearchobjects.
Thereisalackofreliablehistoricaldataforallkindsofthings,anditisimpossibletodeterminehowmanycategoriesthereare.Thepurposeistoclassifythingssimilarinnatureintoonecategory.
Thereisacertaincorrelationbetweentheindicators.
Clusteranalysisisasetofstatisticalanalysistechniquesthatdivideresearchobjectsintorelativelyhomogeneousclusters.Clusteranalysisisdifferentfromclassificationanalysis,whichissupervisedlearning.
Variabletypes:qualitativevariables,quantitative(discreteandcontinuous)variables
Clusteringmethod
1,HierarchicalClustering
Mergemethod,decompositionmethod,dendrogram
2.Non-hierarchicalclustering
Divisionclustering,spectralclustering
Featuresofclusteringmethod:
Clusteringanalysisissimpleandintuitive.
Clusteranalysisismainlyusedinexploratoryresearch.Theresultsoftheanalysiscanprovidemultiplepossiblesolutions.Thechoiceofthefinalsolutionrequiresthesubjectivejudgmentoftheresearcherandfollow-upAnalysis;
Regardlessofwhetherthereareactuallydifferentcategoriesintheactualdata,clusteranalysiscanbeusedtoobtainsolutionsdividedintoseveralcategories;
Thesolutionofclusteranalysisdependsentirelyontheclusteringvariablesselectedbytheresearcher.Addingordeletingsomevariablesmayhaveasubstantialimpactonthefinalsolution.
Researchersshouldpayspecialattentiontothevariousfactorsthatmayaffecttheresultswhenusingclusteranalysis.
Outliersandspecialvariableshaveagreaterimpactonclustering.Whenthemeasurementscalesofcategoricalvariablesareinconsistent,itneedstobestandardizedinadvance.
Ofcourse,whatclusteranalysiscan’tdois:
Automaticallydiscoverandtellyouhowmanyclassesyoushouldbedividedinto—belongingtounsupervisedclassanalysisMethod
Itisunrealistictoexpecttofindroughlyequalcategoriesormarketsegmentsclearly;
Sampleclustering,therelationshipbetweenvariablesneedstobedeterminedbytheresearcher;
p>
Itwillnotautomaticallygiveanoptimalclusteringresult;
TheclusteranalysisImentionedhereismainlyhierarchicalclusteringandfastclustering(K-means)Two-stepclustering(Two-Step);
Accordingtotheclusteringvariables,itisameasurethatdescribesthedegreeofcorrespondenceorclosenessbetweentwoindividuals(orbetweenvariables).
Itcanbemeasuredintwoways:
1.Useindicatorsthatdescribetheclosenessofindividualpairs(variablepairs),suchas"distance",thesmallerthe"distance"Themoresimilartheindividuals(variables).
2.Useindicatorsthatindicatethedegreeofsimilarity,suchas"correlationcoefficient".Thelargerthe"correlationcoefficient",themoresimilarindividuals(variables)are.
Therearemanywaystocalculateclustering-thedistanceindexD(distance):accordingtothedifferentnatureofthedata,differentdistanceindexescanbeselected.Euclideandistance,SquaredEuclideandistance,Manhattandistance(Block),Chebychevdistance,Chi-Squaremeasure,etc.;therearealsomanysimilarities,MainlythePearsoncorrelationcoefficient!
Themeasurementscalesoftheclustervariablesaredifferent,andthevariablesneedtobestandardizedinadvance;
Ifsomeoftheclustervariablesareveryrelevant,Whichmeansthattheweightofthisvariablewillbegreater
ThesquareofEuclideandistanceisthemostcommonlyuseddistancemeasurementmethod;
Theclusteringalgorithmhasagreaterimpactontheclusteringresultsthanthedistancemeasurementmethod;
Thestandardizationmethodaffectstheclusteringmode:
Variablestandardizationtendencyproducesquantity-basedclustering;
Samplestandardizationtendencyproducespattern-basedclustering;
GeneralThenumberofclustersisin4-6categories,whichisnoteasytobetoomuchortoolittle;
Statistics
Clustercenterofgravity
Clustercenter
Distancebetweenclusters
Stratificationsteps
Definetheproblemandchoosecategoricalvariables
Clusteringmethod
Determinethenumberofgroups
Assessmentofclusteringresults
Descriptionandinterpretationofresults
K-means
Itisnon-hierarchicalAkindofclusteringmethod
(1)Executionprocess
Initialization:select(ormanuallyspecify)certainrecordsasaggregationpoints
Circulation:
p>Accordingtotheprincipleofproximity,agglutinatetheremainingrecordstotheaggregationpoint
Calculatethecenterposition(mean)ofeachinitialclassification
Usethecalculatedcenterpositiontore-cluster
Thecycleisrepeateduntilthecondensingpointpositionconverges.
(2)Methodcharacteristics
Usuallyaknownnumberofcategoriesisrequired
Manuallyspecifytheinitialposition
Savecalculationtime
Itisnecessarytoconsiderwhenthesamplesizeisgreaterthan100
Onlycontinuousvariablescanbeused
Process
Features:
Processingobjects:categoricalvariablesandcontinuousvariables
Automaticallydeterminetheoptimalnumberofcategories
Processlargedatasetsquickly
Assumptions:
Variablesareindependentofeachother
Categoricalvariablesobeymultinomialdistribution,continuousvariablesobeynormaldistribution
Themodelisrobust
Principleofthealgorithm
Thefirststep:scanthesamplesonebyone,andeachsampleisclassifiedintothepreviousclassaccordingtothedistancefromthescannedsample,oranewclassisgenerated
Thesecondstepistomergethevarioustypesbasedonthedistancebetweentheclassesinthefirststep,andstopthemergingaccordingtocertainstandards.
DiscriminantAnalysis
Introduction:Discriminantanalysis
Taxonomyisthebasicscienceformankindtounderstandtheworld.Clusteranalysisanddiscriminantanalysisarethebasicmethodsofstudyingtheclassificationofthings,whicharewidelyusedinvariousfieldsofnaturalscience,socialscience,industrialandagriculturalproduction.
DiscriminationanalysisDA
Overview
DAmodel
DA-relatedstatistics
TwogroupsofDA
Caseanalysis
Discriminationanalysis
Discriminationanalysisistofindthediscriminantfunctionbasedonthevariablevaluesthatindicatethecharacteristicsofthingsandtheclassestheybelongto.Accordingtothediscriminantfunction,itisananalysismethodtoclassifythingsofunknowncategory.Thecoreistoexaminethedifferencesbetweencategories.
Discriminationanalysis
Different:Discriminantanalysisandclusteranalysisaredifferentinthatdiscriminantanalysisrequiresthevalueofaseriesofnumericalvariablesreflectingthecharacteristicsofthingstobeknown,andtheclassificationofeachbodyisknown.
DAissuitableforfixedtypevariables(causes)andarbitraryvariables(self)
Twotypes:onediscriminantfunction;
Multiplegroups:morethanonediscriminantfunction
ThepurposeofDA
Establishadiscriminantfunction
Checkwhethertherearesignificantdifferencesinthepredictorvariablesbetweendifferentgroups
DecidewhichpredictionVariablescontributethemosttothedifferencebetweengroups
Classifyindividualsaccordingtopredictorvariables
Analysismodel
FirstestablishthediscriminantfunctionY=a1x1+a2x2+...anxn,where:Yisthediscriminantscore(discriminationvalue),x1x2...xnarevariablesreflectingthecharacteristicsoftheresearchobject,anda1a2...anarethecoefficients
Relatedstatistics
CanonicalCorrelationCoefficient
CharacteristicValue
Wilk's(0,1)=SSw/SStforX
Groupcenterofgravity
Classificationmatrix
Twosetsofdiscriminant
Definitionproblem
EstimatingDAfunctioncoefficients
DeterminethesignificanceofDAfunction
Interprettheresults
Assesseffectiveness
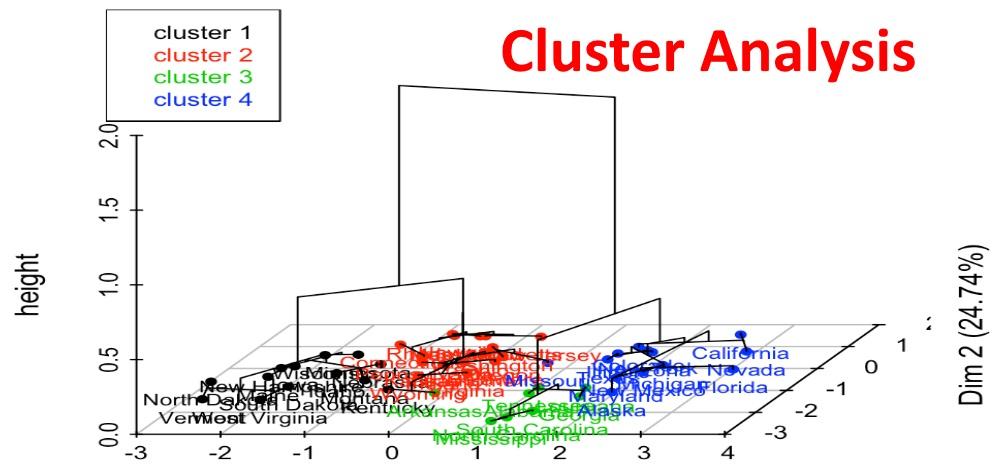
Definetheproblem
Thefirststepofdiscriminantanalysis
ThesecondstepistodividethesampleintoFor:
Analyzethesample
Verifythesample
Estimatethediscriminantfunctioncoefficient
ThedirectmethodistouseallthepredictionsatthesametimeVariableestimationdiscriminantfunction,atthistimeeachindependentvariableisincluded,regardlessofitsdiscriminativeability.Thismethodissuitableforsituationswherepreliminaryresearchortheoreticalmodelsshowwhichindependentvariablesshouldbeincluded.
Stepwisediscriminantanalysis,inwhichpredictorvariablesaregraduallyintroducedbasedontheirabilitytodiscriminategroups.
Determiningsignificance
Nullhypothesis:themeanofalldiscriminantfunctionsofeachgroupinthepopulationisequal.
Characteristicvalue
Typicalcorrelationcoefficient
Wilk's(0,1)convertedtochi-squaretest
Seetravel.spo
Explaintheresult
Thesignofthecoefficientisnotimportant,butitcanexpresstheinfluenceofeachvariableonthevalueofthediscriminantfunctionandtheconnectionwithaspecificgroup.
Wecanpreliminarilyjudgetherelativeimportanceofvariablesbystandardizingtheabsolutevalueofthediscriminantfunctioncoefficients.
Byexaminingthestructuralcorrelationcoefficient,therelativeimportanceofpredictorscanalsobejudged.
Groupcenterofgravity
Assesstheeffectivenessofdiscriminantanalysis
Accordingtotheestimateddiscriminantweightoftheanalyzedsample,multiplyitbythevalueofthepredictorvariableintheretainedsample.Getthediscriminantscoreofeachsampleintheretainedsample.
Canbedividedintodifferentgroupsaccordingtothediscriminantpointsandappropriaterules.
Thehitratio,ortheprobabilityofcorrectclassificationofasample,istheratioofthesumofdiagonalelementsoftheclassificationmatrixtothetotalnumberofsamples.
Comparethesamplecorrectclassificationpercentagewiththerandomcorrectclassificationpercentage.
Factoranalysismodel
Factoranalysismodel(FA)
Basicidea
Factoranalysismodel
ThebasicideaofFA
"Factoranalysis"wasproposedbyThurstonein1931.TheconceptoriginatedfromthestatisticalanalysisofPearsonandSpearmen.
FAusesafewfactorsTodescribetherelationshipbetweenmultiplevariables,thevariableswithhighercorrelationbelongtothesamefactor;
FAuseslatentvariablesoressentialfactors(basiccharacteristics)toexplainobservablevariables
FAmodel
X1=a11F1+a12F2+…+a1pFp+v1
X2=a21F1+a22F2+…+a2pFp+v2X=AF+V
Xi=ai1F1+ai2F2+…+aipFp+vi
Xm=ap1F1+ap2F2+…+ampFm+vm
Xi—theithstandardizedvariable
aip—thefirstThestandardregressioncoefficientsofivariablestothep-thcommonfactor
F—commonfactor
Vi—specialfactor
commonfactormodel
F1=W11X1+W12X2+…+W1mXm
F2=W21X1+W22X2+…+W2mXm
Fi=Wi1X1+Wi2X2+…+WimXm
Fp=Wp1X1+Wp2X2+…+WpmXm
Wi—weight,factorscorecoefficient
Fi—estimatedvalueofthei-thfactor(factorscore)
relatedStatistics
Bartlett'sspheretest:thevariablesareindependentofeachother
KMOvalue:FAsuitability
Factorload:correlationcoefficient
Factorloadmatrix
Commonfactorvariance(degreeofcommonality)
Eigenvalue
Percentofvariance(variancecontributionrate)
Cumulativevariancecontributionrate
Factorloaddiagram
Stonediagram
FAstep
Definetheproblem
TesttheapplicabilityoftheFAmethod
Determinethefactoranalysismethod
Factorrotation
Explainthefactor
Calculatefactorscore
Notes
Thesamplesizeshouldnotbetoosmall
Variablecorrelation
Commonfactorshavepracticalsignificance
Mainapplications
Commercial
ClusteranalysisisusedtofinddifferentcustomersUsergroups,andportraythecharacteristicsofdifferentcustomergroupsthroughthepurchasemodel.
Clusteranalysisisaneffectivetoolformarketsegmentation.Itcanalsobeusedtostudyconsumerbehavior,findnewpotentialmarkets,selectexperimentalmarkets,andserveasapre-processingformultivariateanalysis.
Biology
Clusteranalysisisusedtoclassifyplantsandanimalsandclassifygenestogaininsightsintotheinherentstructureofpopulations
Geography
Clusteringcanhelpthesimilarityofdatabasebusinesstrendsobservedintheearth
Insuranceindustry
ClusteranalysisusesahighaverageconsumptiontoidentifyautoinsurancepolicyholdersSomegroupingsareusedtoidentifyacity’srealestategroupingbasedonhousingtype,value,andgeographiclocation.
Internet
ClusteranalysisisusedtoclassifydocumentsontheInternettorepairInformation
E-commerce
Clusteringanalysisisalsoanimportantaspectinthedataminingofwebsiteconstructionine-commerce.Itclustersoutcustomerswithsimilarbrowsingbehaviorsthroughgrouping,andanalyzesThecommoncharacteristicsofcustomerscanbetterhelpe-commerceusersunderstandtheircustomersandprovidethemwithmoresuitableservices.
Mainsteps
1.Datapreprocessing,
2.Defineadistancefunctiontomeasurethesimilaritybetweendatapoints,
3.Clusteringorgrouping,
4.Evaluatetheoutput.
Datapreprocessingincludesselectionnumber,typeandfeaturescale.Itreliesonfeatureselectionandfeatureextraction.Featureselectionselectsimportantfeatures.Featureextractiontransformstheinputfeatureintoanewsalientfeature.Theyareoftenusedtoobtainasuitablefeaturesetforclusteringinordertoavoidthe"dimensionalitydisaster".Datapreprocessingalsoincludesremovingoutliersfromthedata.Outliersaredatathatarenotattachedtogeneraldatabehaviorsormodels,sotheyareisolated.Pointsoftenleadtobiasedclusteringresults,soinordertogetthecorrectclusters,wemusteliminatethem.
Sincesimilarityisthebasisfordefiningaclass,themeasurementofsimilarityinthesamefeaturespacebetweendifferentdataisveryimportantfortheclusteringstep,duetothediversityoffeaturetypesandfeaturescalesThedistancemeasurementmustbecautious.Itoftendependsontheapplication.Forexample,thedistancemeasurementdefinedinthefeaturespaceisusuallyusedtoevaluatethedissimilarityofdifferentobjects.Manydistancesareusedindifferentfields.Asimpledistancemeasurement,suchasEuclideandistanceisoftenusedtoreflectthedissimilaritybetweendifferentdata.Somesimilaritymeasures,suchasPMCandSMC,canbeusedtocharacterizetheconceptualsimilarityofdifferentdata.Inimageclustering,thesub-imageErrorcorrectioncanbeusedtomeasurethesimilarityoftwographs.
Itisanimportantsteptoclassifydataobjectsintodifferentclasses.Dataisclassifiedintodifferentclassesbasedondifferentmethods.Divisionmethodandhierarchicalmethodarethetwomainmethodsofclusteranalysis.Thedivisionmethodgenerallystartsfromtheinitialdivisionandoptimizationofaclusteringstandard.CrispClustering,eachofitsdatabelongstoaseparateclass;FuzzyClustering,eachofitsdatamaybeinanyclass,CrispClusteringandFuzzyClusterinarethetwomaintechniquesofthedivisionmethod,andthedivisionmethodclusteringisbasedonacertainThisstandardproducesanestedseriesofdivisions,whichcanmeasurethesimilaritybetweendifferentclassesortheseparabilityofaclasstomergeandsplitclasses.Otherclusteringmethodsincludedensity-basedclusteringandmodel-basedclustering.Clustering,grid-basedclustering.
Assessingthequalityofclusteringresultsisanotherimportantstage.Clusteringisanunmanagedprocedureandthereisnoobjectivestandardtoevaluateclusteringresults.Itisevaluatedthroughaclasseffectiveindex.Generallyspeaking,geometricproperties,includingtheseparationbetweenclassesandthecouplingwithinclasses,aregenerallyusedtoevaluatethequalityofclusteringresults.Theclasseffectiveindexoftenplaysanimportantroleindeterminingthenumberofclasses.ThemosteffectiveclassindexisThegoodvalueisexpectedtobeobtainedfromtheactualnumberofclasses.Acommonwaytodeterminethenumberofclassesistoselectthebestvalueofaspecificclasseffectiveindex.WhetherthisindexcantrulygetthenumberofclassesistojudgewhethertheindexisvalidManyexistingstandardscangivegoodresultsforseparatedatasets,butforcomplexdatasets,theyusuallydonotwork,forexample,foroverlappingsetsofdata.
Algorithm
Clusteringanalysisisaveryactiveresearchfieldindatamining,andmanyclusteringalgorithmshavebeenproposed.Traditionalclusteringalgorithmscanbedividedintofivecategories:partitioningmethods,hierarchicalmethods,density-basedmethods,grid-basedmethods,andmodel-basedmethods.
1Partitioningmethod(PAM:PArtitioningmethod)Firstcreatekpartitions,wherekisthenumberofpartitionstobecreated;thenuseacircularpositioningtechniquetohelpbymovingobjectsfromonepartitiontoanotherImprovethequalityofdivision.Typicalclassificationmethodsinclude:
k-means,k-medoids,CLARA(ClusteringLARgeApplication),
CLARANS(ClusteringLargeApplicationbaseduponRANdomizedSearch).
FCM
2Hierarchicalmethod(hierarchicalmethod)Createahierarchytodecomposeagivendataset.Thismethodcanbedividedintotop-down(decomposition)andbottom-up(merge)operationmodes.Inordertomakeupfortheshortcomingsofdecompositionandmerging,hierarchicalintegration
isoftencombinedwithotherclusteringmethods,suchascircularpositioning.Typicalsuchmethodsinclude:
BIRCH(BalancedIterativeReducingandClusteringusingHierarchies)method,whichfirstusesthestructureofthetreetodividetheobjectset;andthenusesotherclusteringmethodstoperformclusteringontheseclusters.optimization.
CURE(ClusteringUsingREprisentatives)method,whichusesafixednumberofrepresentativeobjectstorepresentthecorrespondingcluster;theneachclusteriscontractedbyaspecifiedamount(towardtheclustercenter).
ROCKmethod,whichusestheconnectionbetweenclusterstomergeclusters.
CHEMALOENmethod,whichconstructsadynamicmodelduringhierarchicalclustering.
3Basedonthedensitymethod,theclusteringofobjectsiscompletedaccordingtothedensity.Itcontinuouslygrowsclustersbasedonthedensityaroundtheobject(suchasDBSCAN).Typicaldensity-basedmethodsinclude:
DBSCAN(Densit-basedSpatialClusteringofApplicationwithNoise):Thisalgorithmperformsclusteringbycontinuouslygrowingregionswithsufficientlyhighdensity;itcanextractdatafromspatialdatabasescontainingnoiseFindclustersofarbitraryshapes.Thismethoddefinesaclusterasasetof"densityconnected"points.
OPTICS(OrderingPointsToIdentifytheClusteringStructure):doesnotexplicitlygenerateacluster,butcalculatesanenhancedclusteringorderforautomaticinteractiveclusteranalysis..
4Inthegrid-basedmethod,theobjectspaceisfirstdividedintofiniteunitstoformagridstructure;thenthegridstructureisusedtocompletetheclustering.
STING(STatisticalINformationGrid)isamethodforgrid-basedclusteringusingstatisticalinformationstoredingridcells.
CLIQUE(ClusteringInQUEst)andWave-Clusteraremethodsthatcombinegrid-basedanddensity-basedmethods.
5Amodel-basedapproach,whichassumesamodelforeachclusterandfindsdatasuitableforthecorrespondingmodel.Typicalmodel-basedmethodsinclude:
StatisticalmethodCOBWEB:isacommonlyusedandsimpleincrementalconceptualclusteringmethod.Itsinputobjectisdescribedbysymbolicquantity(attribute-value)pairs.Usetheformofclassificationtreetocreateahierarchicalcluster.
CLASSITisanotherversionofCOBWEB..Itcanperformincrementalclusteringoncontinuouslyvaluedattributes.Itsavesthecorrespondingcontinuousnormaldistribution(meanandvariance)foreachattributeineachnode;andusesanimprovedclassificationabilitydescriptionmethod,thatis,insteadofcalculatingdiscreteattributes(values)likeCOBWEB,thesumisIntegratecontinuousattributes.ButtheCLASSITmethodalsohassimilarproblemswithCOBWEB.Therefore,theyarenotsuitableforclusteringlargedatabases.
Traditionalclusteringalgorithmshavesuccessfullysolvedtheclusteringproblemoflow-dimensionaldata.However,duetothecomplexityofdatainpracticalapplications,existingalgorithmsoftenfailwhendealingwithmanyproblems,especiallyforhigh-dimensionaldataandlarge-scaledata.Becausetraditionalclusteringmethodsmainlyencountertwoproblemswhenclusteringhigh-dimensionaldatasets.①Therearealargenumberofirrelevantattributesinthehigh-dimensionaldataset,whichmakesthepossibilityofclustersinalldimensionsalmostzero;②Thedatainthehigh-dimensionalspaceshouldbesparselydistributedinthelower-dimensionalspace,anditisacommonphenomenonthatthedistancebetweenthedataisalmostequal.Thetraditionalclusteringmethodisbasedondistancetocluster,soitisimpossibletoconstructclustersbasedondistanceinhigh-dimensionalspace.
High-dimensionalclusteranalysishasbecomeanimportantresearchdirectionofclusteranalysis.Atthesametime,high-dimensionaldataclusteringisalsoadifficultpointinclusteringtechnology.Withtheadvancementoftechnology,datacollectionhasbecomeeasierandeasier,leadingtolargerandlargerdatabasesandhighercomplexity,suchasvarioustypesoftradetransactiondata,Webdocuments,geneexpressiondata,etc.,theirdimensions(Attributes)canusuallyreachhundredsorthousandsofdimensions,orevenhigher.However,affectedbythe"dimensionaleffect",manyclusteringmethodsthatperformwellinlow-dimensionaldataspacesareoftenunabletoobtaingoodclusteringresultswhenusedinhigh-dimensionalspaces.Clusteranalysisofhigh-dimensionaldataisaveryactivefieldinclusteranalysis,anditisalsoachallengingtask.High-dimensionaldataclusteranalysishasawiderangeofapplicationsinmarketanalysis,informationsecurity,finance,entertainment,andanti-terrorism.
